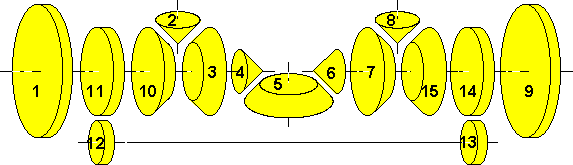
Type "Sleeswyk"

The ultimate design: Prof. Sleeswyk's reconstruction of Wu Tê-jen's historic chariot. It consists of three (!) differentials which are coupled and constrained very cleverly:

The shaft of road wheel 1 is rigidly connected to the shaft of bevel gear 2.
Likewise road wheel 9 moves the shaft of bevel gear 8. Note that there is no main axle !
The shaft of wheel 5 - which carries the pointer on its upper end - is mechanically held vertical at all times.

The basic equations (see equation for generic differential):

(a:)	n₃ * rot₃ + n₁₀ * rot₁₀ - (n₃ + n₁₀) * rot₁ = 0
(b:)	n₇ * rot₇ + n₁₅ * rot₁₅ - (n₇ + n₁₅) * rot₉ = 0
(c:)	n₆ * rot₆ - n₅ * rot₅ = 0
(d:)	n₄ * rot₄ + n₅ * rot₅ = 0 (POV to the far right !)
(e:)	n₁₁ * rot₁₁ + n₁₂ * rot₁₂ = 0
(f:)	n₁₃ * rot₁₃ + n₁₄ * rot₁₄ = 0

The other constraints in math notation:

(g:)	rot₃ = rot₄
(h:)	rot₆ = rot₇
(i:)	rot₁₀ = rot₁₁
(j:)	rot₁₂ = rot₁₃
(k:)	rot₁₄ = rot₁₅

Composition (POV is from top respectively from far right):

(k=>)	rot₁₅ = rot₁₄
(f=>)	= (-1) * (n₁₃ / n₁₄) * rot₁₃
(j=>)	= (-1) * (n₁₃ / n₁₄) * rot₁₂
(e=>)	= (n₁₃ / n₁₄) * (n₁₁ / n₁₂) * rot₁₁
(i=>l:)	= (n₁₃ / n₁₄) * (n₁₁ / n₁₂) * rot₁₀
(a=>)	rot₁₀ = ((n₃ + n₁₀) / n₁₀) * rot₁ - (n₃ / n₁₀) * rot₃
(g,d=>)	= ((n₃ + n₁₀) / n₁₀) * rot₁ + (n₃ / n₁₀) * (n₅ / n₄) * rot₅
(b=>)	rot₁₅ = ((n₇ + n₁₅) / n₁₅) * rot₉ - (n₇ / n₁₅) * rot₇
(h,c=>)	= ((n₇ + n₁₅) / n₁₅) * rot₉ - (n₇ / n₁₅) * (n₅ / n₆) * rot₅
(l=>)	rot₁₅ = (n₁₃ / n₁₄) * (n₁₁ / n₁₂) * ((n₃ + n₁₀) / n₁₀) * rot₁ + (n₁₃ / n₁₄) * (n₁₁ / n₁₂) * (n₃ / n₁₀) * (n₅ / n₄) * rot₅
(m:)	[(n₁₃ / n₁₄) * (n₁₁ / n₁₂) * (n₃ / n₁₀) * (n₅ / n₄) + (n₇ / n₁₅) * (n₅ / n₆)] * rot₅ + (n₁₃ / n₁₄) * (n₁₁ / n₁₂) * ((n₃ + n₁₀) / n₁₀) * rot₁ - ((n₇ + n₁₅) / n₁₅) * rot₉ = 0

To make it "south-pointing" requires, that if rot₉ is held 0, rot₅ has to be exactly one turn when wheel 1 of diameter d₁ covered one full circle (centre at wheel 1's contact to the ground, radius equal to track width t):

(n:)	d₁ * rot₁ * PI = 2 * t * PI
(o:)	rot₅ = 1
(p:)	rot₁₂ = 0
(m=>)	rot₁ = (-1) * [(n₁₃ / n₁₄) * (n₁₁ / n₁₂) * (n₃ / n₁₀) * (n₅ / n₄) + (n₇ / n₁₅) * (n₅ / n₆)] * (n₁₄ / n₁₃) * (n₁₂ / n₁₁) * (n₁₀ / (n₃ + n₁₀))
(n=>)	d₁ = 2 * t / \| rot₁ \|

The same method can be applied to calculate the required size for wheel 9: If rot₁ is held 0, rot₅ has to be exactly one turn when wheel 9 of diameter d₉ covered one full circle (this time centre at wheel 1's contact to the ground, radius equal to track width t):

(q:)	d₉ * rot₉ * PI = 2 * t * PI
(r:)	rot₁ = 0
(m=>)	rot₉ = [(n₁₃ / n₁₄) * (n₁₁ / n₁₂) * (n₃ / n₁₀) * (n₅ / n₄) + (n₇ / n₁₅) * (n₅ / n₆)] * (n₁₅ / (n₇ + n₁₅))
(q=>)	d₉ = 2 * t / rot₉

Given Parameters (Your choice !)

Reference	Size	Description
2	n₂ = [teeth]	Bevel gear, shaft fixed to wheel 1
3	n₃ = [teeth]	Bevel gear, freerunning on horizontal shaft
4	n₄ = [teeth]	Bevel gear, fixed to wheel 3
5	n₅ = [teeth]	Bevel gear, carries pointer on vertical shaft
6	n₆ = [teeth]	Bevel gear, free running on horizontal shaft
7	n₇ = [teeth]	Bevel gear, fixed to wheel 6
8	n₈ = [teeth]	Bevel gear, shaft fixed to road wheel 9
10	n₁₀ = [teeth]	Bevel gear, free running on horizontal shaft
11	n₁₁ = [teeth]	Spur gear, fixed to wheel 10
12	n₁₂ = [teeth]	Spur gear, fixed to auxiliary shaft
13	n₁₃ = [teeth]	Spur gear, fixed to auxiliary shaft
14	n₁₄ = [teeth]	Spur gear, freerunning on horizontal shaft
15	n₁₅ = [teeth]	Bevel gear, fixed to wheel 14
T	t = [length units]	Track width

Derived Parameters

Reference	Size	Description
1	d₁ = [units of t]	Roadwheel, fixed on axle
9	d₉ = [units of t]	Roadwheel, fixed on axle