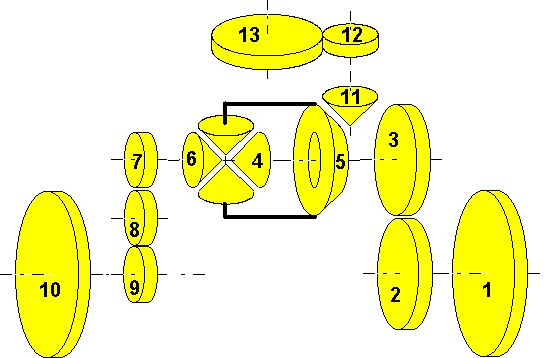

As usual, the dimensioning equations:
| (a:) | rot4 + rot6 - 2 * rot5 = 0 |
| (b:) | n2 * rot2 + n3 * rot3 = 0 |
| (c:) | n7 * rot7 + n8 * rot8 = 0 |
| (d:) | n8 * rot8 + n9 * rot9 = 0 |
| (e:) | n5 * rot5 - n11 * rot11 = 0 |
| (f:) | n12 * rot12 + n13 * rot13 = 0 |
| (g:) | rot1 = rot2 |
| (h:) | rot3 = rot4 |
| (i:) | rot6 = rot7 |
| (j:) | rot9 = rot10 |
| (k:) | rot11 = rot12 |
| (b,g,h=>) | rot4 = - (n2 / n3) * rot1 |
| (c,d,i,j=>) | rot6 = (n9 / n7) * rot10 |
| (e,f,k=>) | rot5 = -(n11 / n5) * (n13 / n12) * rot13 |
| (a=>l:) | 2 * (n11 / n5) * (n13 / n12) * rot13 = (n2 / n3) * rot1 - (n9 / n7) * rot10 |
| (m:) | d10 * rot10 * PI = 2 * t * PI | d1 * rot1 * PI = 2 * t * PI | |
| (n:) | rot1 = 0 | rot10 = 0 | |
| (o:) | rot13 = -1 | rot13 = 1 | |
| (l=>) | rot10 = (n7 / n9) * (n11 / n5) * (n13 / n12) | rot1 = k * (n3 / n2) * (n11 / n5) * (n13 / n12) | |
| (m=>) | d10 = 2 * t / rot10 | d1 = 2 * t / rot1 |